Cohesive Construction
Source: Gustavino's Book Cohesive Construction
Two Methods of Analysis:
-
Elastic Method:
-
Material strength
-
Material elasticity
-
-
Equilibrium Method:
-
Geometry
-
Self-Weight
-
Reason for Equilibrium Analysis:
“Both theories arrive to same conclusion: the safety of a masonry structure is a matter of geometry. A safe state of equilibrium is achieved through a correct geometry. Both historically and theoretically the "equilibrium approach" is the best approach to the analysis and design of masonry structures.” [Source: Mechanics of masonry vaults: The equilibrium approach by Santiago Huerta, Pg 1]
“The analysis of such structures can be approached by either equilibrium methods or by elastic methods. The former depends on the geometry and self-weight of the structure to determine its stability, while the latter evaluates the structure based on its material strength and elasticity… This section provided a logical conclusion that the equilibrium methods are better suited to analyze masonry domes compared to elastic methods…” [Source: Structural Assessment of the Guastavino Masonry Dome of the Cathedral of Saint John the Divine by Hussam Dugum, Pg 28]. Following this argument we tried to analyze our structure using the equilibrium method.
Our Assumption:
-
No tensile strength
-
Infinite compressive strength
-
No sliding failure
STRUCTURAL ANALYSIS OF MASONRY VAULTS
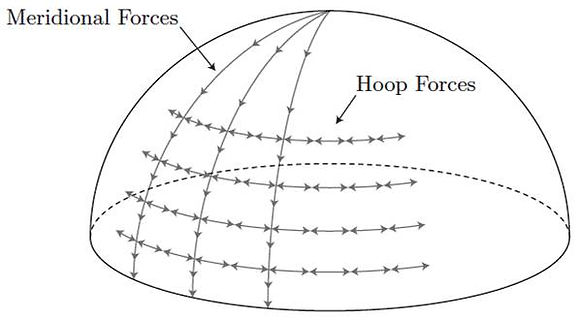
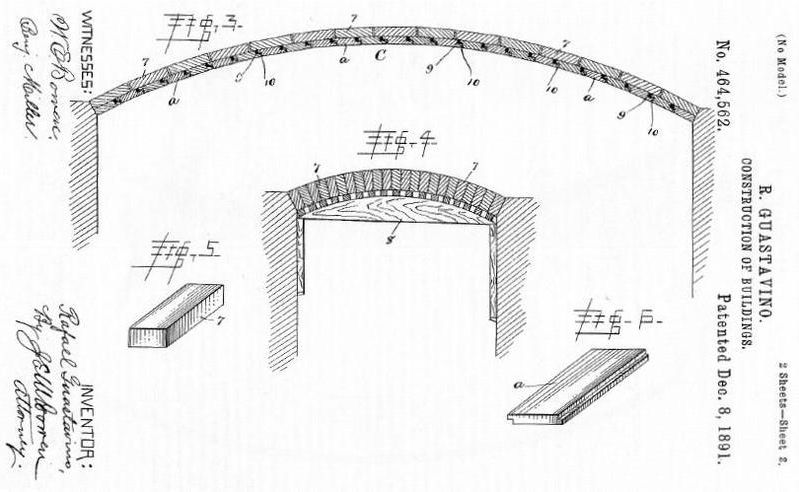
[Source: Structural Assessment of the Guastavino Masonry Dome of the Cathedral of Saint John the Divine by Hussam Dugum, Pg 24]
There are Meridional and Hoop forces in a dome. However since a vault is an extrusion of an arch along one axis it would not experience Hoop stresses. Hence, for our vault we assume that we only have Meridional Forces and no Hoop Forces acting on it.
Given:
Span: 4.57 m
Rise: 0.447 m
Arc length: 4.71 m

Total Load according to our case:
Total dead load (with an assumed thickness of 75mm) = 1943.3 kg/m
Total live load = 250kg/m^2 x 4.57 = 914 kg/m
Total load (D.L + L.L) = 2857 kg/m
Factor of safety = 1.2
Total load = 3428.4 kg/m
Since the arch is symmetrical, we can calculate the loads on half the arch and replicate it on the other half.
Hence load on half the arch = 3428.4/2 = 1714.2 kg/m
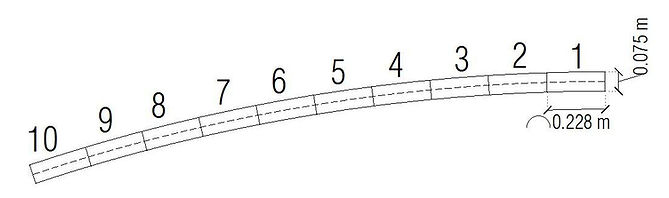
Divide half arch into 10 equal segments with the assumed 0.075 m thickness:
-
Find the center of each of the segments.
-
Make a horizontal to each of the centers.
-
Find the angle (o) the tangent of the curve at the center makes to the horizontal line.
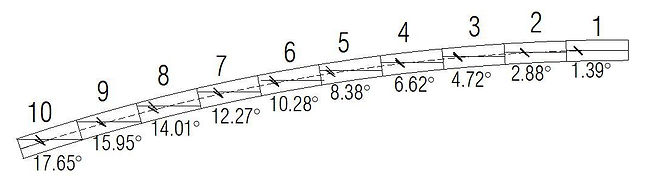
Meridional stress, No = Wr/1+cos (o)
W = weight per unit area
The UDL acting on the arch would also be divided into 10 equal parts:
1714.2/10 = 171.42 kg/m = W
r = radius of the segmental arch = 7.045 m
o = the angle of the curve to the horizontal
Where No can be multiplied to the width of the element to find the Force.
[Source: Structural Assessment of the Guastavino Masonry Dome of the Cathedral of Saint John the Divine by Hussam Dugum, Pg 24]
We get a data table from this:

From the force at each segment we can find the vertical and horizontal component of the force at each of the segments.
F x cos(o) = Horizontal component
F x sin(o) = Vertical component

We can plot them on a graph by joining the respective horizontal to the vertical component to form a graph as show below:
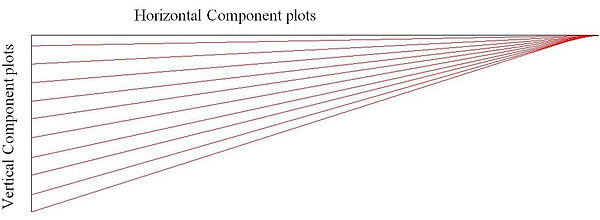
-
Now we plot each of these lines back to their respective segment.
-
Extend each line to match each other and this becomes our thrust line for our vault.


-
Thrust line is contained within 6.4mm of the segmental arch.
-
We consider the thrust line to be in the center 1/3rd of the thickness of the vault.
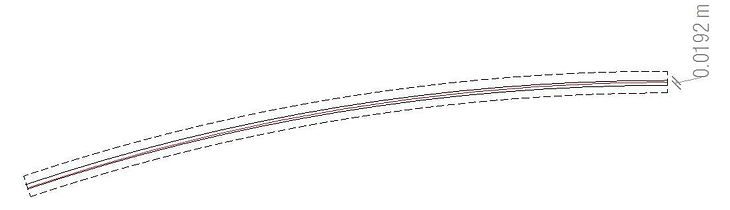
Theoretically, without considering the material’s compressive strength the vault requires a minimum thickness of 19.2mm.
OPTIMIZATION OF THE NUMBER OF LAYERS
There is a non – conclusive test conducted in Laboratory of Meccanica dei Materiali e delle Strutture, the Department of Civil, Environmental, Aerospace, Materials Engineering of the University of Palermo. Some of their findings could have lead to some conclusive evidence however they did not have a large enough sample size. [Source: Tradition and modernity of catalan vaults: Historical and structural analysis, Pg 8].
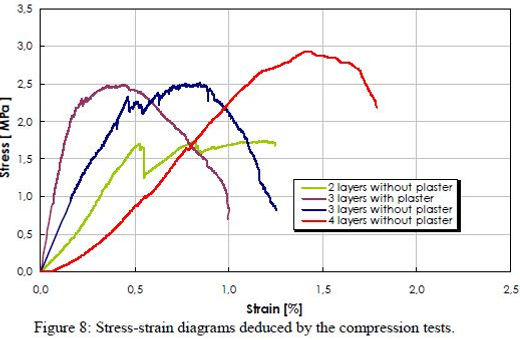
[Source: Tradition and modernity of catalan vaults: Historical and structural analysis, Pg 9].
Findings from the graphical data:
-
The sample, 3 layers with plaster, gives the maximum efficiency in terms of taking a high percentage of stress and gives minimum strain.
-
4 layers without plaster takes maximum stress however gives an equally large percentage of strain as well which would require more lateral strengthening of the walls through buttresses or tie rods.
-
The sample of 3 layers without plaster does perform better than the sample of 2 layers without plaster, so >2 layers of masonry is required.
Since these are not conclusive we can only assume than 3 layers with plaster gives better efficiency than 4 layers and our walls would experience minimum lateral thrust.